Just as a (very) quick recap, I started from a simple Stack in part-1 and ended up creating a fully functioning RpnCalculator in part-2 and part-3. In this part, I will try to focus on two things-
- Ability to add mathematical operations from outside.
- Ability to handle unary operations.
But, I will first clean up the module and namespace declaration a little. It got messy as I was not paying attention to it at all. I decided to have a single namespace for a single project (Stack, RpnCalculator, etc.). Within these namespaces, there will be types declared that I want to expose automatically when I use the namespaces. Also, the namespaces will contain relevant module declaration within themselves. So, Stack namespace will have a type Stack<’a> defined inside along with the module Stack. That will ensure some consistency in the module and namespace names. Also, I have to write Stack.push and Stack.pop now, which is looks more meaningful. Finally, I have to fix the tests to compile with this new form. The changes I made for Stack and Stack.Tests projects can be found here.
Since the re-arranging of namespace and module for Stack makes it looks cool, I want to do the same for RpnCalculator too. I placed RpnCalculator and RpnResult type declarations in the RpnTypes.fs file, outside any module declaration. I also made the RpnBinaryOperation module internal inside the RpnCalculator namespace. Needless to say, I have to add proper prefix in test codes too to compile them and run. Exact detail of the changes I made can be found in this commit detail.
Lets get down to business and create something awesome. It is about time I start using RpnCalculator type that I have defined since forever! Looking at it, looks like I don’t need any stack within the calculator. Because, I will be passing the stack as a parameter to the calculate method. So, after removing the stack, the RpnCalculator type looks like:
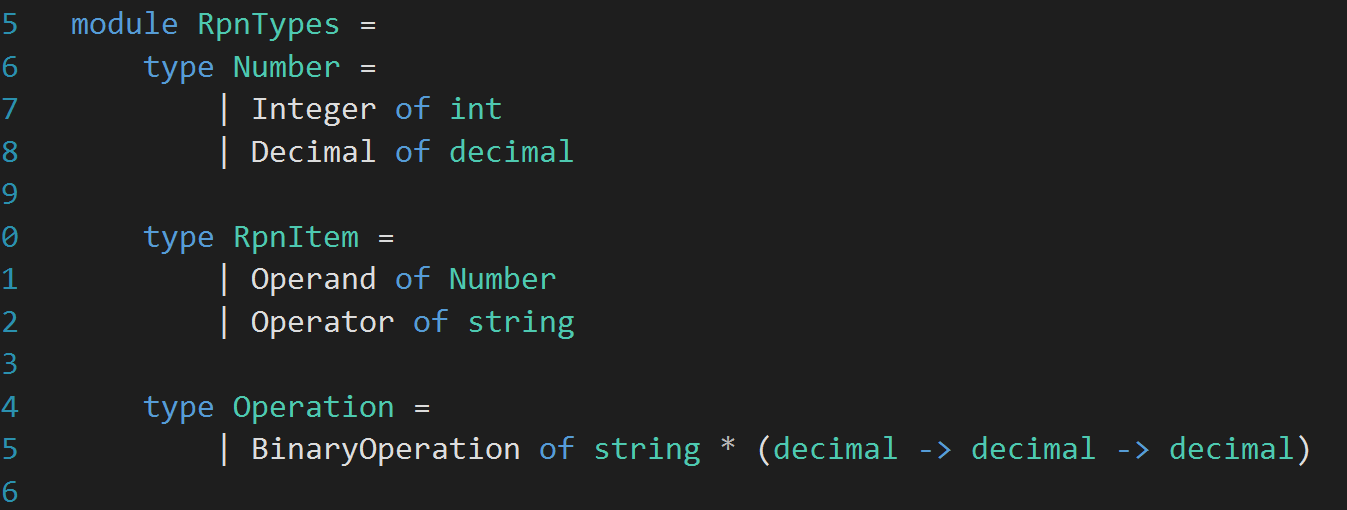
I also realize that all the operations I have defined so far takes two decimal numbers as input and returns a decimal as output. So, let’s change the type definition for Operation to match that. Here is how the whole RpnTypes module looks like:
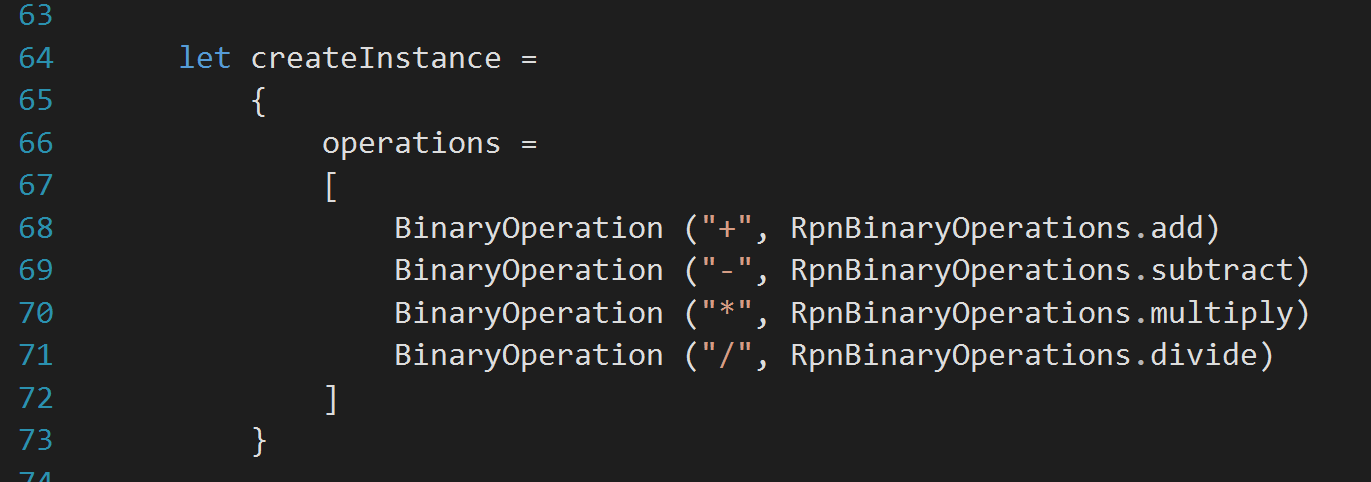
Much meaningful now and I feel like I can use it pretty soon. I am adding a new method in RpnCalculator.fs file, right before calculate method, to get a new instance of RPN calculator. Here it is:
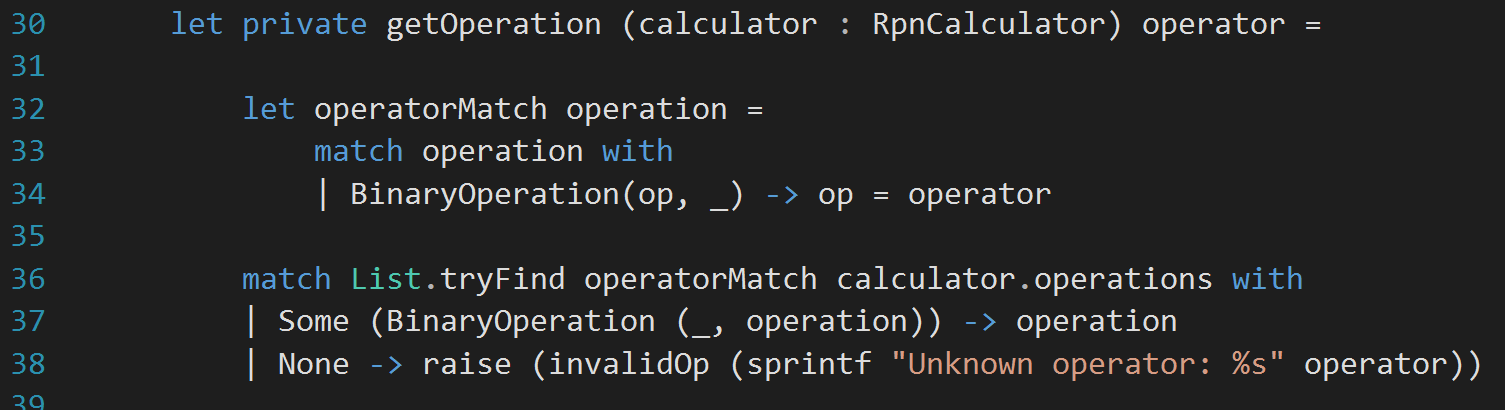
Looks pretty simple. I haven’t actually changed anything to affect the calculate method so far. But, it is good a idea to run the tests often. With all the tests green, now I want to pass a calculator object to the calculate function. The reason behind this would be to access the list of operations I have in the calculator object. For this reason, I definitely need the object passed into the getOperation method. Let’s change the signature (not the implementation) like:
getOperation is only called from evaluateRpnExpr. The requirement of passing the calculator object immediately forces the change in implementation of evaluateRpnExpr to include calculatorstack as the first parameter, instead of simply *stack. It looks like:
Important thing to note that, I also need change return type from the function to calculatorstack* to make it suitable for List.fold. Now, I changed the calculate method a bit to match the signature of the list folder (i.e. evaluateRpnExpr method) and passed null as a calculator. Here is how:
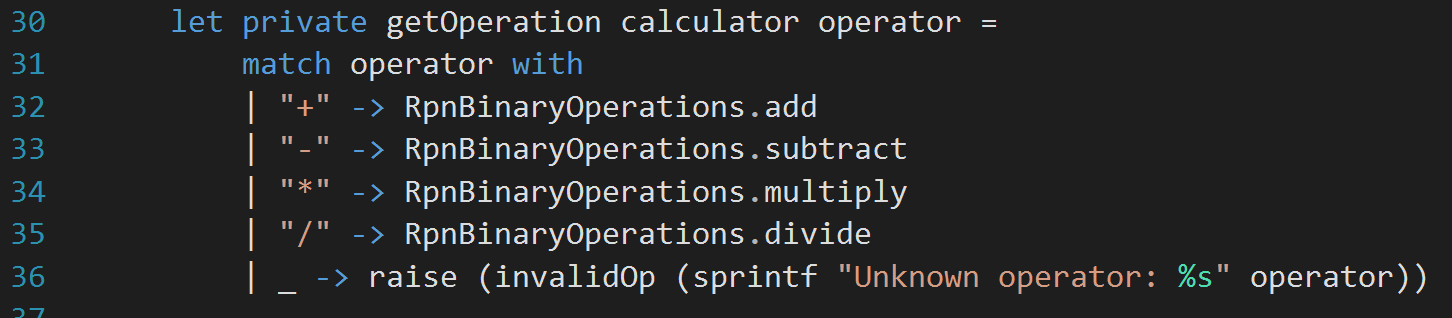
I have the projects compiling now. First thing is to run the tests. Phew! they are all green. With the confidence of the tests I have, I am now going to use an actual calculator now to figure our the operation for a symbol, instead of previous static mapping. So, my modified getOperation method looks like:
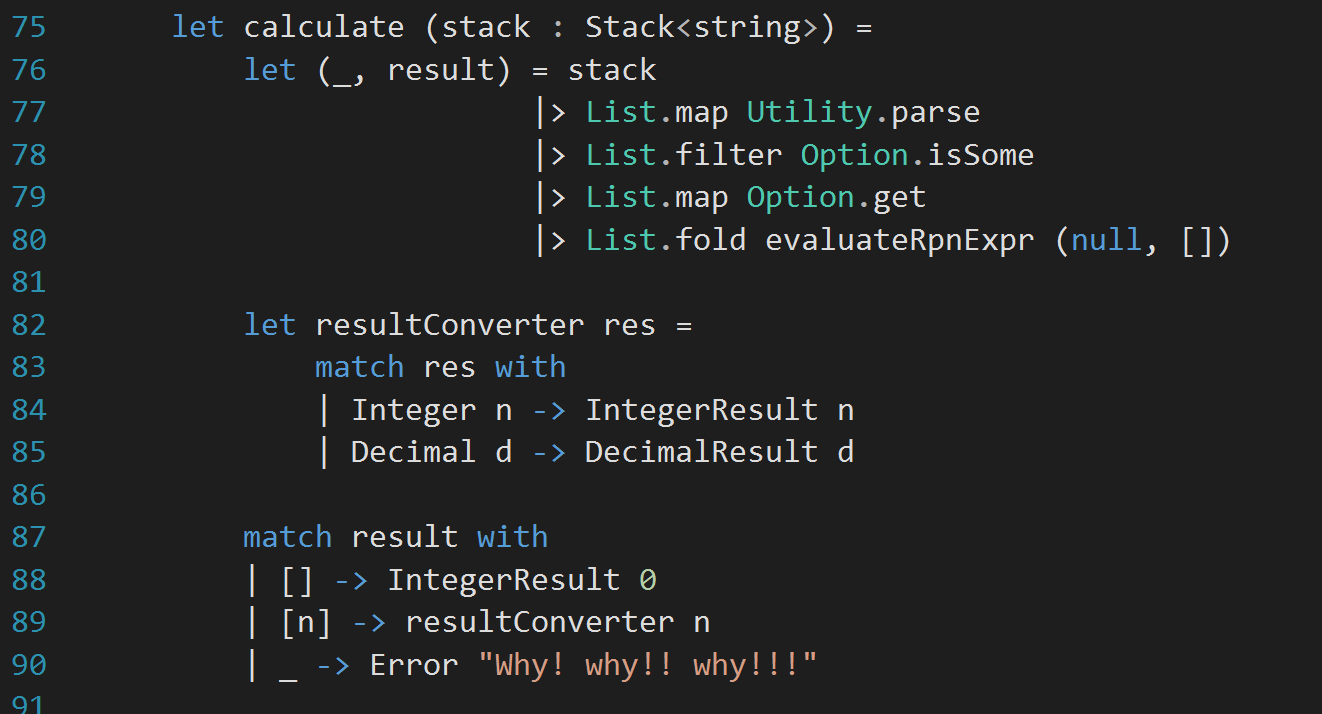
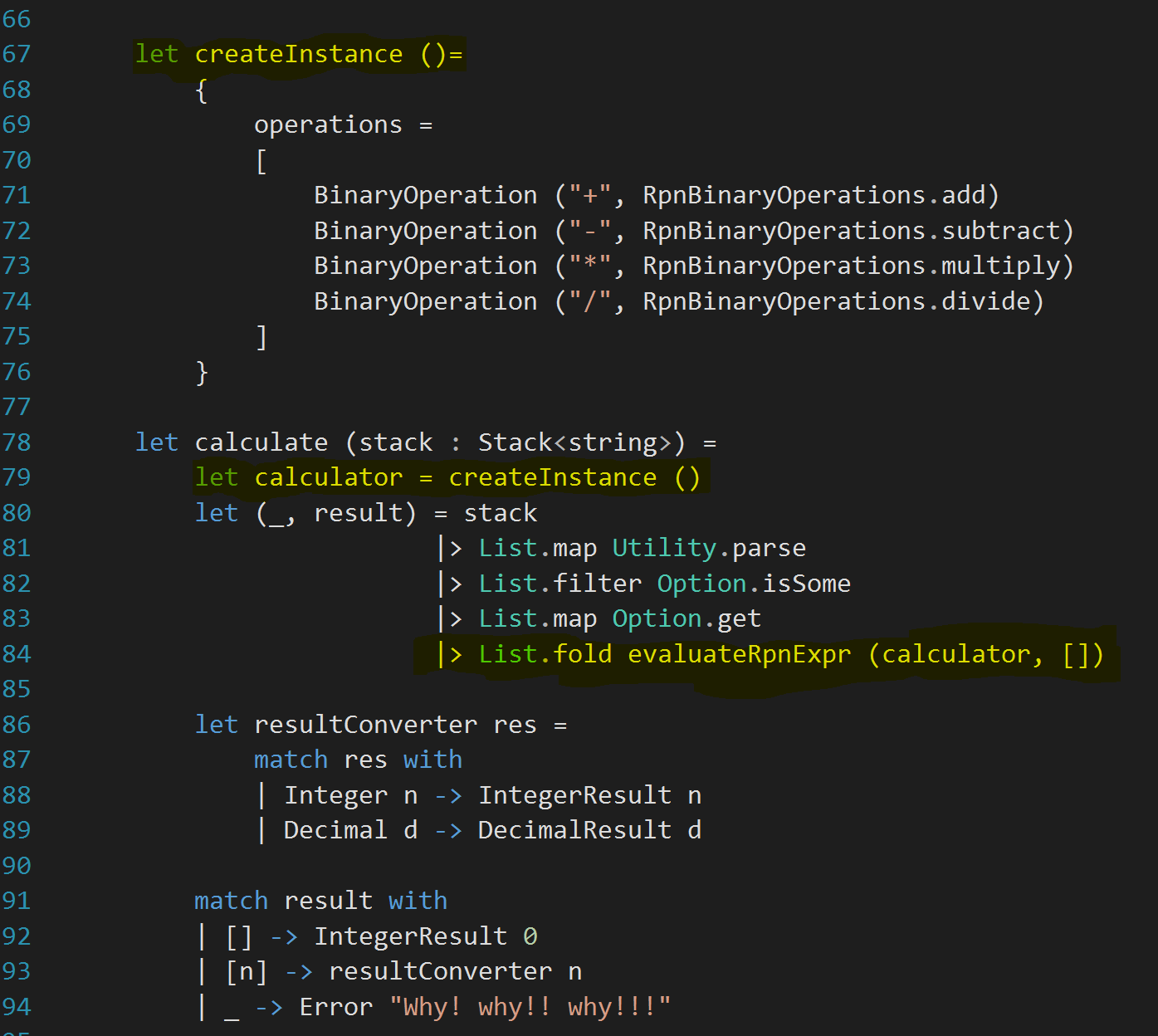
Now, I have to pass in the real calculator from calculate method. So, fixing a small mistake in createInstance method, the new calculate method looks like (changes are highlighted in yellow):
Amazingly, all tests are green. :)
Now, I am ready to pass in calculator from outside world to the calculate method. So, I changed the signature of the method as:
This will make all the tests fail to compile. So, I am going to cheat a little with TDD and pass in RpnCalculator.createInstance() as the newly introduced parameter. The changes I made can be found in this commit detail. It immediately makes the tests pass. How cool is that!
Now, I am going to rock the world (of RpnCalculator). I am adding a new method of, called registerBinaryOperation, with the expectation that it will take an operator symbol, operation definition for the symbol and a calculator. In return, it will give the calculator back where the new operator/operation is known. A simplest dummy-compiler-friendly implementation of such method would be:
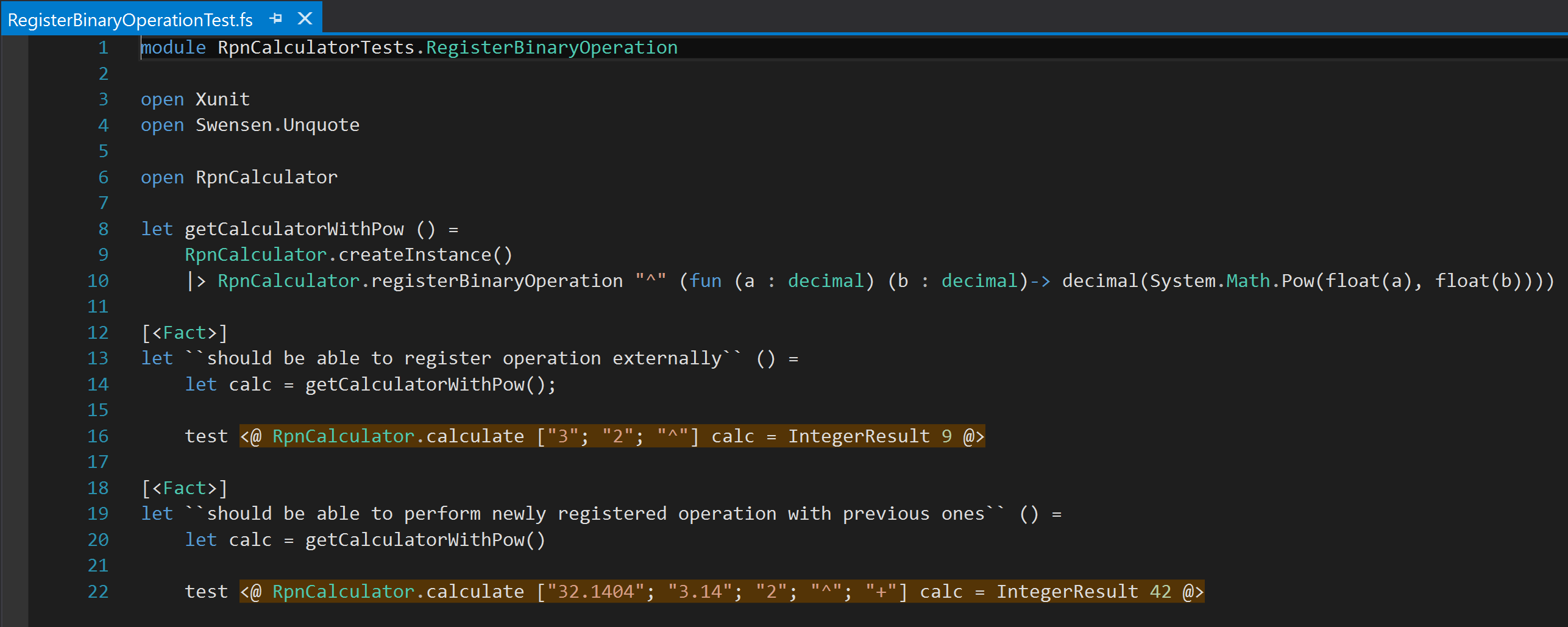
I placed this method in the RpnCalculator.fs file, right above the calculate method. I added a new test file to define the behavior of this method in a new file named RegisterBinaryOperationTest.fs in the RpnCalculator.Tests project. And, the test cases look like:
Well, the test helper method getCalculatorWithPow( ) may look a bit scary. That is not my fault (!). Math.Pow can take float inputs and return float output. But, I need decimal. So, lot of explicit type conversions are in place, that’s all. Important thing is, I am passing a symbol and an operation to register in the calculator as a known operation. Tests look fine, except they all fail. Unknown operator: ^. Well, that is the exception message that I throw from calculator when an unknown operator is found. So, it is obvious that the new operator registration is not working with the dummy implementation I have. Let’s change it to a proper implementation as:
When I run my tests now, all are passing. Amazing. That marks the end of first part.
In the next part, I will try to add the ability to handle unary operators like neg, sqr, sqrt, etc. So, as before, I add a method like:
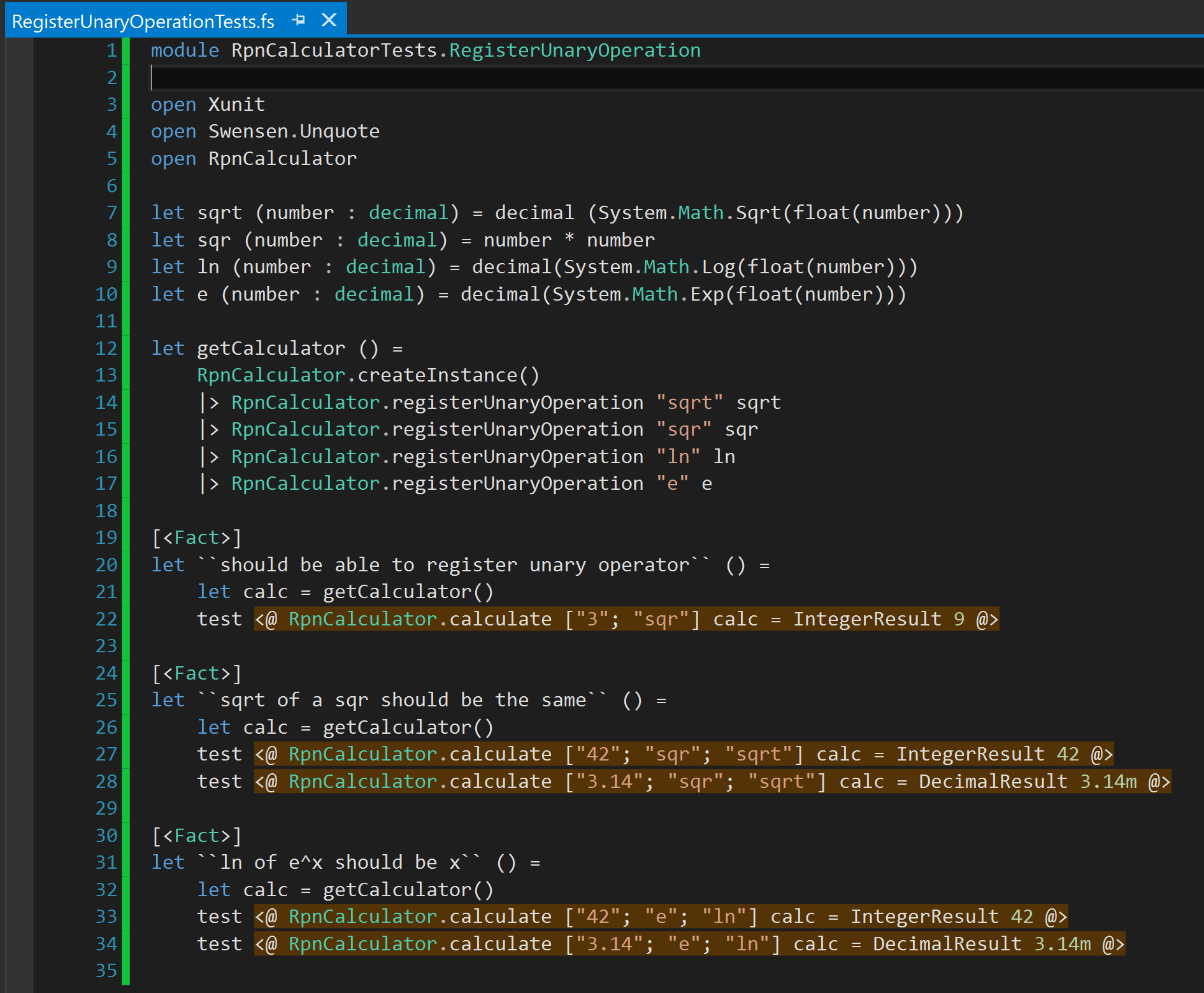
This lets me write tests I want. So, I add a new file named RegisterUnaryOperationTests.fs with the following tests:
Tests looks nice, but, as expected, they all fail. Because, I haven’t really implemented the registerUnaryOperation method properly. To do that, first I will need to introduce a new type of operation in my discriminated union type Operation. Obviously it looks like:
After looking at the code which is currently responsible for doing “operation”, I came up with the following implementation that can support both unary and binary operators. Here is the new implementation of “operation” section of the module:
Here, applyBinaryOperands and applyUnaryOperand methods are returning decimal now. The applyOperation method is taking care of proper method to call, stack manipulation and conversion of result type. I think it will be easier to understand the changes if we can see what has changed from previous version. This commit detail will help with understanding the changes. I have also implemented the registerUnaryOperation method properly, replacing the previous dummy implementation. It looks like:
Now, when I run the tests, all passes except one particular test that tries to state that, ln(e^x) == x. Well, in my test case, I have used x = 42. Looking detail inside test failure message, I found that it is actually failing to convert a very large number from decimal to integer inside operandConversion method. And, the very large decimal being e^42. It indicates that I need to add some checks in this method to stop overflow or underflow errors like this. So, the improved method definition looks like:
And, all my tests are shining green. :)
That’s all for this part. In the next part, I will either spend some time on optimization or will step into the implementation of a calculator for infix notation (how people write mathematical expressions).
Useful links
- GitHub repository: fsharp-tdd-calculator
- Link to other parts: README section of the repository









Comments